type 1 and type 2 errors
먼저 알아야할 것은 귀무가설과 대립가설. 느낌적으로 구분할 필요가 있는데, $H_{0}$는 테스트하는 가설(그래서 검정통계량을 $H_{0}$ 기준으로 낸다). $H_{1}$는 $H_{0}$를 reject할 경우의 가설. ‘귀무가설을 기각한다, 귀무가설을 기각할 수 없다’라고 표현하지, ‘대립가설을 채택한다’라고 하면 혼난다.
내용적으로 풀어보면 이게 우연인지 아닌지, 아니라면 얼마나 차이가 있는건지를 확인한다. 그래서 대부분 $H_{0}: \mu=0$이 된다.
AB test 예시를 보면 다 2개의 봉우리를 그린다. 각각 A, B의 분포를 그리는데 꼭 교집합이 있어서 우릴 힘들게 한다. 교집합이 type 1, 2 error의 주범인데 이는 평균이 달라 생기는 문제다. 평균이 얼마나 다르냐에 따라 교집합 영역이 바뀌게 된다. 이 평균 차이를 영어로 effect size라 부른다. 최소 얼마만큼 차이 안나면 인정 안한다는 의미로 보면 된다. (학부 때 영어로 안 배워서 나중에 구글링이 힘들었다)
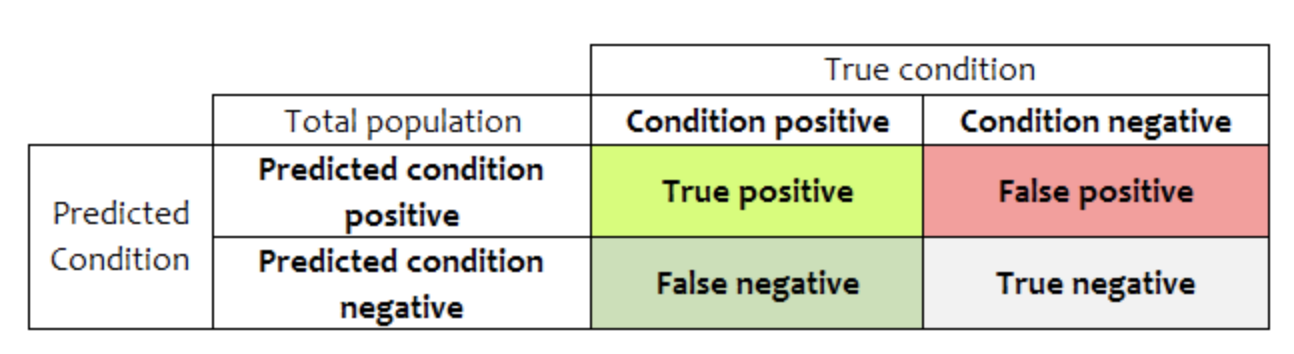
confusion matrix로 보면 암이 있다 1, 없다 0일 때 type 1은 $H_{0}$인데 $H_{1}$이라고 한거니까 암이 없는데 있다고 한 것.(false positive)
type 2는 $H_{1}$인데 $H_{0}$이라고 한거니까 암이 있는데 없다고 한 것.(false negative)
(학부떈 암이 없다가 0인게 이해가 안됐는데, 귀무가설이 뭔지를 감을 잡으면 납득이 된다.)
rule of thumb으로 alpha = .05, power = .8로 잡는다. 즉 beta는 .2라는 것이고 alpha보다 4배 크게 잡는다는 것이다. 이는 type 1 error를 type 2보다 훨씬 보수적으로 잡는다는 걸 알 수 있다. (암이 아닌데 암 치료 받는 것 * 4 = 암인데 암이 아니라고 하는 것)
사실 생각해보면 sample size가 100,000이 넘어간다면 추론의 오차가 매우 작아져서 이런 방식의 t test는 필요 없다고 생각한다. ex) 푸시 캠페인 반응
하루가 아닌 여러 날짜에 거쳐 진행하는 AB test의 경우에는 날짜별로 $N$이 다르거나 sample의 특성이 다르기 때문에 t test보다는 베이지안 방식의 AB test를 이용하는 게 좋을 것 같다. ex) 추천로직 변경