type 1 and type 2 errors

이번 포스팅의 교재

먼저 알아야할 것은 귀무가설과 대립가설. 느낌적으로 구분할 필요가 있는데, $H_{0}$는 테스트하는 가설(그래서 검정통계량을 $H_{0}$ 기준으로 낸다). $H_{1}$는 $H_{0}$를 reject할 경우의 가설. ‘귀무가설을 기각한다, 귀무가설을 기각할 수 없다’라고 표현하지, ‘대립가설을 채택한다’라고 하면 혼난다.

내용적으로 풀어보면 이게 우연인지 아닌지, 아니라면 얼마나 차이가 있는건지를 확인한다. 그래서 대부분 $H_{0}: \mu=0$이 된다.

AB test 예시를 보면 다 2개의 봉우리를 그린다. 각각 A, B의 분포를 그리는데 꼭 교집합이 있어서 우릴 힘들게 한다. 교집합이 type 1, 2 error의 주범인데 이는 평균이 달라 생기는 문제다. 평균이 얼마나 다르냐에 따라 교집합 영역이 바뀌게 된다. 이 평균 차이를 영어로 effect size라 부른다. 최소 얼마만큼 차이 안나면 인정 안한다는 의미로 보면 된다. (학부 때 영어로 안 배워서 나중에 구글링이 힘들었다)

confusion matrix로 보면 암이 있다 1, 없다 0일 때 type 1은 $H_{0}$인데 $H_{1}$이라고 한거니까 암이 없는데 있다고 한 것.(false positive)
type 2는 $H_{1}$인데 $H_{0}$이라고 한거니까 암이 있는데 없다고 한 것.(false negative) (학부떈 암이 없다가 0인게 이해가 안됐는데, 귀무가설이 뭔지를 감을 잡으면 납득이 된다.)

rule of thumb으로 alpha = .05, power = .8로 잡는다. 즉 beta는 .2라는 것이고 alpha보다 4배 크게 잡는다는 것이다. 이는 type 1 error를 type 2보다 훨씬 보수적으로 잡는다는 걸 알 수 있다. (암이 아닌데 암 치료 받는 것 * 4 = 암인데 암이 아니라고 하는 것)

사실 생각해보면 sample size가 100,000이 넘어간다면 추론의 오차가 매우 작아져서 이런 방식의 t test는 필요 없다고 생각한다. ex) 푸시 캠페인 반응
하루가 아닌 여러 날짜에 거쳐 진행하는 AB test의 경우에는 날짜별로 $N$이 다르거나 sample의 특성이 다르기 때문에 t test보다는 베이지안 방식의 AB test를 이용하는 게 좋을 것 같다. ex) 추천로직 변경

attenutaed bias - 과소 추정

단순 회귀 모형을 상정하여 $Y=\tilde{X}\beta_{1}$에서 $\tilde{X}=X+w$라고 하자. true $X$를 기준으로 $\hat{\beta}$은 $\frac {\sigma_{x}} {\sigma_{x} + \sigma_{w}}$만큼 작은 값을 가지는 과소 추정 문제 발생. (수식은 길어서 생략. 정규방정식의 $X^\prime X$로 second moment 문제가 된다는 것만)

직관적으로 보면 아주 당연하다는 생각.

simultaneity - 동시성

개념은 서로가 서로의 설명변수인 관계. (피자를 먹으면 콜라가 먹고 싶고, 콜라를 먹으면 피자를 먹고 싶은 그런 느낌)
핵심은 현상을 더욱 잘 설명하는 omitted variable을 찾으라.

• 양말과 냉장고 판매량은 인과관계가 없을텐데, 상관계수가 높아서 그냥 쓰는 경우. 사실은 둘이 동시에 프로모션을 했다. (회사 분석계에도 이런 프로모션 피처가 있으면 좋겠다😟)
• 초콜릿 소비량과 노벨상 수상자의 상관계수처럼 그냥 상관계수만 높은 경우.

sampling

모수: parameter
인데 sample 개수와 모수를 혼동하시는 분이 많아서 나까지 흔들리고 있다😅

sample bias를 피하려면 1. random sampling, 2. apple to apple
A/B test를 예로 들면 접속 순서대로 A,B,A,B.. 배정하면 random OK, 그룹 간 동질성이 있다고 할 수 있으므로 apple to apple OK.

t test

t 검정 수식의 분모에 집중해 보자.

1. pooled variance건 unpooled건 결국 분산의 합이다.
   • $V(\bar{X_1}) + V(\bar{X_2})$ 과 똑같다.
2. balanced일수록 error가 적다.
   • $N_1=N_2$일 때 $\sqrt{\frac{1}{N_1}+ \frac{1}{N_2}}$가, 그리고 검정 에러가 최소화된다. A/B test에서 balanced sample size를 하는 이유가 여기있다!

📓이번주는 수리통계가 안 나와서 수월했다. 나쁜 추정에 대한 개념을 통해 내가 했던 지난 실수들을 새로운 맥락에서 볼 수 있는 것이 오늘의 성과.

데이터 사이언스 강의를 들으려는 찰나에 질문을 받아서 어쩔 수 없이 다시 공부한 회귀분석

이번주에는 반드시 데이터 사이언스 인강를 듣고 정리 포스팅을 올리려 했는데, 카카오톡을 보니 동생이 회귀분석 질문을 보낸게 아닌가. 다행히 회귀분석은 첫 전공수업이어서 굉장히 열심히 했던 추억이 있다. 그래도 막상 보니 생각이 안 나는게 많아 다시 공부하며 시간을 보냈다. 그래서 결국 강의 요약은 또 다음 주로…😢 오늘 공부한 내용을 정리해본다.

문제

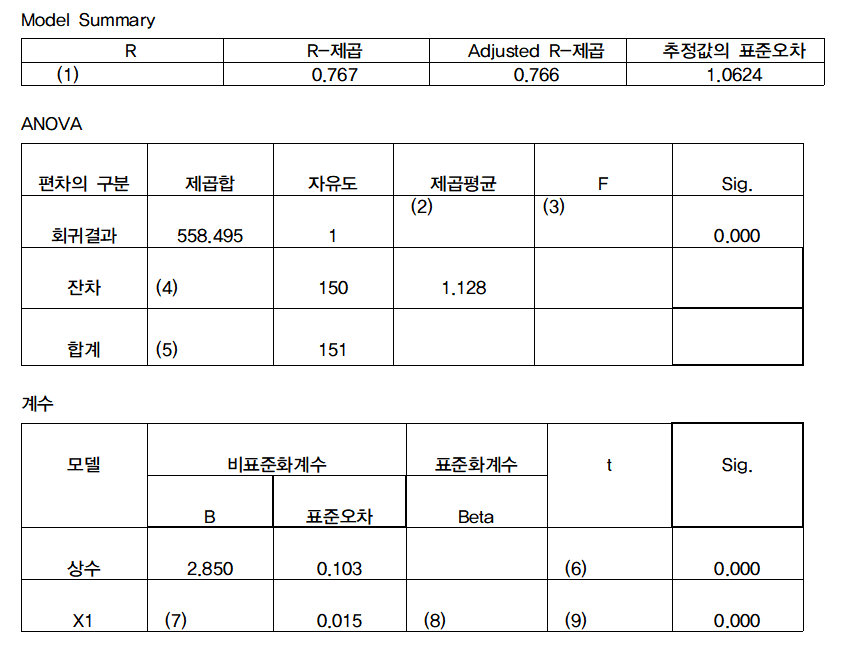
학부 때 시험 문제로 자주 나올만큼 의미있는 문제다. 하지만 알아도 쓸모가 없는 문제라고 생각하기 때문에 이런 건 괴롭지 않게 적당히 좀 내줬으면 좋겠다.

너무 쉬운 2, 4, 5는 생략하고 1번은 피처가 1개인 단순회귀에서 특징으로 $R^2$가 $correlation(x, y)^2$ 라는 점을 이용한다. 3번은 f분포의 특성인 분산의 비율을 구하라는 것이다. 자세히는 몰라 설명은 어렵다. (다음엔 이걸로 공부해서 올리는 걸로) 정답은 제곱평균의 비율로 (2)/1.128.

6, 9번은 t 통계량으로 $\frac{coef - 0}{s.e.}=\frac{2.850-0}{0.103}$ (왜 t 통계량을 쓰는 지는 링크참조)

대망의 7번은 숨은 그림 찾기하듯 풀어야된다. $\beta = \frac {\sum (x-\bar{x}) (y-\bar{y})} {\sum (x-\bar{x})^2}$ 이기 때문에 핵심은 $\sum (x-\bar{x}) (y-\bar{y})$ 와 $\sum (x-\bar{x})^2$ 를 어디서 찾을 것이냐다.

결론만 말하면 $\sum (x-\bar{x})^2$는 $\sigma^2$에서, $\sum { (x-\bar{x}) (y-\bar{y}) }$는 $r$에서 찾아야 된다. 코드로 상세 설명을 대신한다.

n = 152
n1 = 151

sigma = 1.0624
sigma2 = sigma ** 2

standard_error_beta = .015

sse = 1.128 * 150
syy = sse + 558.495

# sxx = sum of square (x - xbar)
# sxy = sum of (x - xbar)(y - ybar)
# standard_error_beta == (1.128 / sxx) ** .5
sxx = 1.128 / (standard_error_beta ** 2)

vx = sxx / n1
vy = syy / n1

r2 = .767
# r2 = sxy2 / sxx syy
sxy2 = r2 * sxx * syy
sxy = sxy2 ** .5
beta = sxy / sxx
print(beta)

상관계수와 회귀계수의 관계

내가 답을 처음에 준게 0.0002로 아주 작은 수였다. 코드를 잘못짜서 나온 값이었고 지금은 0.33이 나오지만 어찌됐건 이런 질문을 했다. 상관계수가 0.85가 넘는데 회기계수가 그렇게 작을수가 있냐고. 사실 수식만 보면 알 수 있는데 답은 yes다. x의 분산이 y보다 크면 $\beta$ 값이 작아져서 0처럼 보일 수 있다.

예시를 만들어서 해보니 정말로 그렇다.

import random

import numpy as np

n = 150
samples = np.array([[random.uniform(10, 20) for i in range(n)],
              [random.uniform(10, 20) for i in range(n)]]).T

correlation_matrix = np.array([[1, .99], [.99, 1]])
samples = samples @ np.linalg.cholesky(correlation_matrix) @ np.linalg.cholesky(correlation_matrix) \
        @ np.linalg.cholesky(correlation_matrix)

x = samples[:, 0]
y = samples[:, 1]

corr = lambda x, y: np.corrcoef(x, y)[0, 1]
print('corr: ', corr(x, y))

covmat = np.cov(x, y)
vx = covmat[0, 0]
vy = covmat[1, 1]

sx = vx ** .5
sy = vy ** .5

slope1 = (np.cov(x, y)[0, 1] / vx)
slope2 = (corr(x, y) * sy / sx)


from sklearn import linear_model

mdl = linear_model.LinearRegression().fit(x.reshape(-1, 1), y)
slope3 = mdl.coef_[0]
print('slope: ',slope1)

상관계수는 0.7491인데 회귀계수는 0.001이 나올 것이다. 그렇다고 이 계수가 꼭 버려지지는 않는게, 숫자가 작은 만큼 오차도 작아 회귀계수에 대한 t 검정이 유의하다고 나올 수 있다.

새삼스레 다시 느끼지만 회귀분석도 깊이 들어가면 한도 끝도 없이 어려워진다.